#P1713E. Cross Swapping
Cross Swapping
Description
You are given a square matrix $A$ of size $n \times n$ whose elements are integers. We will denote the element on the intersection of the $i$-th row and the $j$-th column as $A_{i,j}$.
You can perform operations on the matrix. In each operation, you can choose an integer $k$, then for each index $i$ ($1 \leq i \leq n$), swap $A_{i, k}$ with $A_{k, i}$. Note that cell $A_{k, k}$ remains unchanged.
For example, for $n = 4$ and $k = 3$, this matrix will be transformed like this:

The operation swaps the blue row with the green column.
You can perform this operation any number of times. Find the lexicographically smallest matrix you can obtain after performing arbitrary number of operations.
For two matrices and of size , let and . Then, the matrix is lexicographically smaller than the matrix when there exists an index () such that a_i < b_i and for all indices such that 1 \leq j < i, .
给定一个 的矩阵。一次操作可以给定一个 然后交换所有的 和 。
如图表示 的情况。
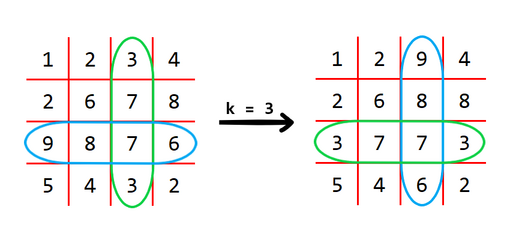
求若干次操作后字典序最小的矩阵。
Input
The first line contains a single integer $t$ ($1 \leq t \leq 10^5$) — the number of test cases.
The first line of each test case contains a single integer $n$ ($1 \leq n \leq 1000$) — the size of the matrix.
The $i$-th line of the next $n$ lines contains $n$ integers $A_{i, 1}, A_{i, 2}, \dots, A_{i, n}$ ($1 \le A_{i, j} \le 10^9$) — description of the matrix $A$.
It is guaranteed that the sum of $n^2$ over all test cases does not exceed $10^6$.
Output
For each test case, print $n$ lines with $n$ integers each — the lexicographically smallest matrix.
2
3
2 1 2
2 1 2
1 1 2
4
3 3 1 2
1 1 3 1
3 2 3 2
2 3 3 1
2 1 1
2 1 1
2 2 2
3 1 1 2
3 1 2 1
3 3 3 3
2 3 2 1
5
6
4 25 2 3 15 8
23 19 28 7 22 18
0 3 12 6 19 17
20 18 9 16 15 8
6 23 17 28 12 29
10 26 15 8 15 28
9
26 2 15 23 9 20 13 21 0
20 0 20 14 15 20 25 17 29
16 23 1 10 23 0 6 6 29
0 5 20 27 9 17 4 8 25
17 11 29 7 13 11 2 6 6
5 22 29 20 17 15 2 28 12
24 18 3 15 14 8 25 17 20
10 9 16 5 29 6 29 12 21
17 13 4 8 7 21 6 17 4
10
19 3 16 27 4 14 21 27 15 27
23 13 17 13 27 4 18 12 29 13
13 17 7 4 20 18 15 18 4 21
14 4 14 8 10 3 15 16 22 28
12 17 2 5 6 0 18 17 21 11
2 16 23 29 18 18 12 24 10 10
3 17 16 22 2 12 27 27 21 20
21 18 13 27 29 21 18 24 15 18
9 14 8 6 13 15 16 0 15 3
25 5 1 16 22 3 11 17 0 13
6
26 11 21 3 29 26
28 11 25 16 23 25
15 7 14 6 2 28
20 19 22 19 0 11
5 9 29 3 3 0
18 20 1 16 6 13
8
14 6 15 13 21 11 27 4
11 5 10 3 29 22 2 1
3 24 0 20 27 3 11 11
21 7 12 24 21 26 29 22
27 12 0 13 4 11 16 28
23 15 22 12 0 1 27 16
20 19 7 13 21 13 21 19
19 12 18 5 12 2 18 26
4 23 0 3 6 8
25 19 28 18 22 26
2 3 12 9 19 15
20 7 6 16 28 8
15 23 17 15 12 15
10 18 17 8 29 28
26 2 15 0 9 5 13 10 0
20 0 20 5 15 22 25 9 29
16 23 1 20 23 29 6 16 29
23 14 10 27 7 17 15 8 8
17 11 29 9 13 17 2 29 6
20 20 0 20 11 15 8 28 21
24 18 3 4 14 2 25 29 20
21 17 6 5 6 6 17 12 17
17 13 4 25 7 12 6 21 4
19 3 13 14 4 2 3 21 9 25
23 13 17 4 27 16 17 18 14 5
16 17 7 4 2 18 15 18 4 21
27 13 14 8 5 3 15 16 22 28
12 17 20 10 6 18 2 29 13 22
14 4 23 29 0 18 12 24 10 10
21 18 16 22 18 12 27 27 21 20
27 12 13 27 17 21 18 24 15 18
15 29 8 6 21 15 16 0 15 3
27 13 1 16 11 3 11 17 0 13
26 11 15 3 5 18
28 11 7 16 9 20
21 25 14 22 2 28
20 19 6 19 3 16
29 23 29 0 3 0
26 25 1 11 6 13
14 6 3 13 21 11 20 4
11 5 24 3 29 22 19 1
15 10 0 12 0 22 11 18
21 7 20 24 21 26 13 22
27 12 27 13 4 11 21 28
23 15 3 12 0 1 13 16
27 2 7 29 16 27 21 18
19 12 11 5 12 2 19 26
Note
Note that in every picture below the matrix is transformed in such a way that the blue rows are swapped with the green columns.
In the first test case, we can perform $1$ operation for $k = 3$. The matrix will be transformed as below:



