二分

---

二分是一种常见的非常巧妙的算法，经常为解题打开突破口。 二分的基础的用法就是在单调序列或单调函数中进行查找，当问题的答案具有单调性时，就可以通过二分转化为判定（判定的难度小于求解），使得二分应用范围变得很广泛，还可以扩展到三分法去解决单峰函数的极值以及相关问题。

二分实现方法，但其细节之处确实需要仔细考虑，对于整数值上的二分，需要注意终止边界、左右区间取舍的开闭情况，如果处理不当，很容易造成漏掉答案或造成死循环；对于实数域上的二分，需要注意精度问题。

我们这里介绍二分的倍增写法，本写法来自于艾庆兴老师的智慧，很多学生称为“aqx二分”。

---

二分查找经典模型：

模型1：在单调递增序列 $a$ 中查找第一个大于等于 （$\ge$）$x$ 的数的位置。

分析： 常见的二分查找使用循环不断缩小查找范围，但是需要想清楚边界细节问题，我们可以将此问题换一种思考方式。

如果需要查找的数的位置为 $pos$，也就是 $a[1]...a[pos-1]$ 都小于 $x$ ，即序列 $a$ 序列分成了两段，前一段 $a[1]...a[pos-1]$ 都小于 $x$ ，后一段大于等于 $x$，那就可以从位置 $0$ 往后走，以快的方式走到位置 $pos-1$ (不能直接走到 $pos$ 位置，如果有多个等于 $x$ 的数，无法判断是否为第一个),然后再 $+1$ ,就可以走到 $pos$ 位置。

即就转化为从 $0$ 开始走到 $pos-1$ 位置，任意一个整数都可以表示为二进制，意味着，可以以 $2^i$ 倍增的方式往前试探,如果当前位置 +$2^i$ 对应的数小于 $x$ ,即此处在 $1...pos-1$ 位置上，可以加入，否则不能加入。

即：目标位置 $pos$ ,当前位置初始为 $now=0$ ，取一个比较大的 $2^i$ ，若 $a[now+2^i] \le x,now+=2^i$ ，否则不加，然后试探长度减半，即 $2^i$ 变为 $2^{i-1}$ ,直到试探长度为 $0$。

如查找序列长度为 $n$,初始 $2^i \ge n$ ,可得 $i=\left \lceil log_2 n \right \rceil$,那么 $now=\sum_{i=\left \lceil log_2 n \right \rceil}^{0} q_i*2^i$ ,其中 $q_i=\{0,1\}$,$now$ 可以覆盖 $[1,n]$ 中每一个数，即可以试探到区间 $[1,n]$ 每一个位置，证明了算法的正确性，也可以得到算法复杂度为 $O(logn)$。

参考代码：

	//长度为n的递增序列a中查找第一个大于等于x的位置
   int now=0;
	for(int i=(1<<30);i;i>>=1)    // i初值2^30 >= 序列长度n 
		if(now+i<=n && a[now+i]<x)now+=i;
	now++;
	cout<<now;

模型2：在单调递增序列 $a$ 中查找第一个大于 （$>$）$x$ 的数的位置。

分析： 如果等于也加入，那么 $now$ 就会移动到等于 $x$ 最后一个位置，然后再 $+1$，就是第一个大于 $x$ 的位置。

   //长度为n的递增序列a中查找第一个大于等于x的位置
   int now=0;
	for(int i=(1<<30);i;i>>=1)    // i初值2^30 >= 序列长度n 
		if(now+i<=n && a[now+i]<=x)now+=i;
	now++;
	cout<<now;

实际上模型1和模型2 库中有标准函数可以调用：

lower_bound/upper_bound 二分

lower_bound 查找第一个大于等于目标x的位置，upper_bound 查找第一个大于目标x的位置：

1.在有序int数组（数组存放下标1~n）中查找大于等于x的最小整数的下标：

  int i=lower_bound(a+1,a+n+1,x)-a;

2.在有序vector中查找x的前驱（小于x的最大整数），假设序列中一定存在x

  int y=*--lower_bound(a.begin(),a.end(),x);

例题1：P2249 【深基13.例1】查找

分析：在递增序列上可以利用二分找到第一个大于等于x的位置，判断如果此时对应的数如果不等于x，就说明原序列里面没有这个数，返回 -1 。 本题序列长度 $n=10^6,2^{20} \ge n$ ，因此试探长度就可以从 $2^{20}$ 开始。

int search(int x)
{
	int now=0;
	for(int i=(1<<20);i;i>>=1)
		if(now+i<=n && a[now+i]<x)
			now+=i;
	now++;
	if(a[now]==x)return now;
	else return -1;	
}

例题2： P1102 A-B 数对

分析：统计序列中满足 $A-B=C$（$C$已知）个数，如果枚举序列中的每一个数 $A$ ，就相当于查找序列中查找有多少个 $C+B$ ，为了提高效率，可以将效率排序，然后在有序的序列上查找等于 $C+B$。

那么在就是在递增序列中查找等于 x 的个数，模型 1：查找第一个大于等于 x 的位置，模型 2：查找第一个大于x的位置，两个位置的差就是 x 的个数。

参考代码：点击

---

二分答案转化为判定

对于很多最优化问题，直接求最优解可能很困难，但是如果存在可行解与其评价函数之间存在某种单调关系，那就可以将求最优解问题转变为判定问题。

自变量对应的“定义域”就是该问题的可行解，对可行方案计算得到的评估数值就是因变量，如果自变量与因变量存在单调关系，不妨设评估分越高越优，最优解就是评估值最优的方案。

假设最优解的评估值是 $g$ ,对于 $>g$ 的值，都不存在一个合法的方案达到该评分，否则 $g$ 就不是最优解；而对于 $<g$ 的值，一定存在一个合法方案达到或超过该评分，那么问题的值域就具有一种特殊的单调性---在 $g$ 一侧不合法、在另一侧不合法，可以通过二分找到这个分解点 $g$ 。

例题3：P1182 数列分段 Section II

对于给定的一个长度为N的正整数数列 $A_{1\sim N}$ ，现要将其分成 $M( M \le N )$ 段，并要求每段连续，且每段和的最大值最小。(显著特点最大值最小)

分析： 题目中“最大值最小”，这是答案具有单调性，可用二分转化为判定的最常见、最典型的特征之一。

如果将“每段数字之和”作为自变量，那么能分成“段数”是因变量，它们之间是一种递减关系,如下图。

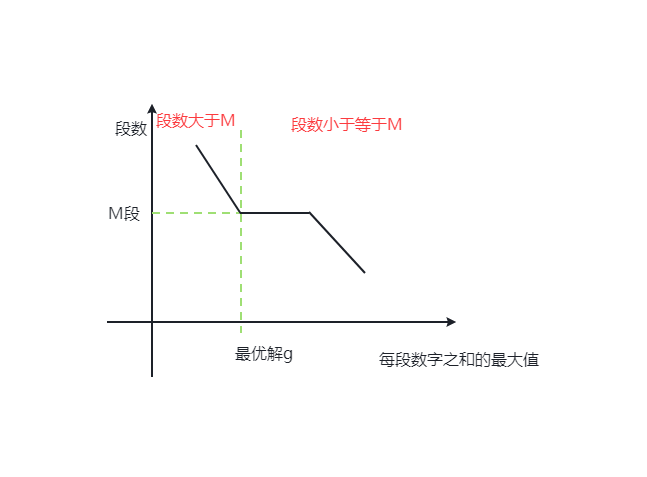
参考代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m,a[N];
int cal(long long  x)
{
	int cnt=1;
	long long sum=0;
	for(int i=1;i<=n;i++)
	{
		if(a[i]>x)return 1e9;
			if(sum+a[i]<=x)sum+=a[i];
		else cnt++,sum=a[i];
	}
	return cnt;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	long long ans=0;
	for(long long i=(1ll<<50);i;i>>=1)
			if(cal(ans+i)>m)ans+=i;
	ans++;
	cout<<ans;
	return 0;
}

---

3.实数域上的二分

实数域上的二分相对而言，简单一些，需要确定好精度 $eps$ ，如果当前值为 $now$ (实数类型)，目标值为 $g$ ,当 $|g-now|<eps$ 时，$now$ 就为目标。

如果在 $[0,l]$ 的区间里存在某种单调关系，就可以用二分，依然可以采用倍增形式实现，步长就是实数类型，初值为 $l$, $now= {\textstyle \sum_{i=l}^{i<eps}} p_i *i,p_i=\{0,1\}$ ,其中下一个 $i=i/2.0$ , $i$ 和 $now$ 都为实数类型，$now$ 可以覆盖 $[0,l]$ 上任意位置。

double now=0;
for(double i=l;i>=eps;i=i/2)
	if(check(i+now))now+=i;
cout<<now;     //不需要加1

例题4：P1577 切绳子

分析： “切割后每条绳子的最大长度”与“能切割的条数”之间存在递减的关系，可以“二分答案”，若“切割后每条绳子”长度小，那么能切割的绳子条数就大于等于题目要求的 $K$ 条，需要变大，反之切割后每条绳子”长度太大，切割条数就不够 $k$ 条，需要变小。

参考代码：点击

三分

三分主要用于解决单峰函数求峰和谷，常规方法，就是在区间中分出两个中值点，然后讨论。

实数上的三分：

double l = L, r = R;
while(r-l>=eps)
{
    double lmid = l + (r - l) / 3, rmid = r - (r - l) / 3;
    if(f(lmid) < f(rmid)) l = lmid;
    else r = rmid;
}
double ans = f(l);
//或 ans=l

整数上的三分：

long long l = L, r = R;
while(r - l > 3) {
    long long lmid = l + (r - l) / 3, rmid = r - (r - l) / 3;
    if(f(lmid) < f(rmid)) l = lmid;
    else r = rmid;
}
long long ans = f(l);
for(int i = l + 1; i <= r; i ++) ans = max(ans, f(i));

时间复杂度：

由于每次搜索域缩减到 $\frac{2}{3}$,即 $T(n)=T(\frac{2}{3}n)+O(1)$ ,因此时间复杂度为 $O(\log_{\frac{3}{2}}\frac{R-L}{eps})$ 。

当然对于连续函数，对于单峰函数，由于存在导数，且导数是单调的，可以将三分转为二分解决。

P3382 【模板】三分法

思路一：

对于函数 $y=f(x+eps)-f(x)$ 是单调的，波峰位置 $y$ 趋近 $0$ ,小于波峰，函数 $y>0$,大于波峰 $y<0$ ，那么可以转化为二分。注意：此处 {eps} 是 {x} 的极小增量，要足够小，取 $eps=10^{-10}$ 。 参考代码：

#include<bits/stdc++.h>
using namespace std;
const int N=15;
const long double eps=1e-10;
long double l,r,a[N];
int n; 
long double f(long double x)
{
	double ret=0;
	for(int i=n;i>=0;i--)
		ret=ret*x+a[i];
	return ret;
}

long double cal(long double x)
{
	double eps=1e-10;  //增量要足够小，否则x和x+eps会跨越峰值分界点，造成错误 
	return f(x+eps)-f(x);
}
int main()
{
	cin>>n>>l>>r;
	for(int i=n;i>=0;i--)cin>>a[i];
	
	long double ans=l;
	for(long double i=r-l;i>=eps;i=i/2)
		if(ans+i<=r && cal(ans+i)>0)ans+=i;
	
	cout<<ans;
	
	return 0;
}    
// 原题中数据加强了，使用 long double,提高精度

思路二

传统三分，对于区间 $[L,R]$,取 $x_1=(L+R)/2,x_2=(x_1+R)/2$，循环比较 $f(x1)$ 与 $f(x2)$ 的大小，直到 $R-L < eps$ 停止.

using namespace std;
const int N=15;
const double eps=1e-6;
double l,r,a[N];
int n; 
double f(double x)
{
	double ret=0;
	for(int i=n;i>=0;i--)
		ret=ret*x+a[i];
	return ret;
}
int main()
{
	cin>>n>>l>>r;
	for(int i=n;i>=0;i--)cin>>a[i];
	
	double x1,x2;
	while(fabs(r-l)>=eps)
	{
		x1=(l+r)/2;
		x2=(x1+r)/2;
		if(f(x1)<f(x2))l=x1;      //区间减少1/4 
		else r=x2;            //区间减少1/2 
	}
	cout<<l;
	return 0;
}                     

思路三

单峰连续函数，其导函数必然单调，波峰位置倒数趋近于 $0$，可以求 $f[x]$ 的导数，然后二分求峰值。

---

1.P2678 [NOIP2015 提高组] 跳石头

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int l,n,m,d[N]; 
int cal(int len) //最短跳跃距离不超过 len，移走石头的数量
{
	int cnt=0,last=0;  //cnt移走石头的数量，last上一次停留的位置
	for(int i=1;i<=n;i++)
		if(d[i]-last<len)cnt++; //i石头要移走
		else last=d[i];
    if(l-last<len)cnt++;   //最后一块石头与终点太近，最后这块石头移走 
	return cnt; 
} 
int main()
{
	cin>>l>>n>>m;
	for(int i=1;i<=n;i++)cin>>d[i];
	int ans=0;
	for(int i=1<<30;i;i=i>>1)
		if(cal(ans+i)<=m)ans+=i;
	cout<<ans;
   return 0;
}

2.P1281 书的复制

#include<bits/stdc++.h>
using namespace std;
const int N=510;
int n,a[N],k; 
int cal(int x)
{
	int cnt=1,sum=a[1];
	for(int i=2;i<=n;i++)
		if(a[i]+sum<=x)sum+=a[i];
		else cnt++,sum=a[i];
	return cnt;
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>a[i];
	int ans=0;
	for(int i=1<<30;i;i=i>>1)
		if(cal(ans+i)>k)ans+=i;
	ans++;
	//cout<<ans<<endl;
	//system("pause");
	int r[N]={0},person=1,sum=0;
	r[1]=n,sum=a[n];
	
	for(int i=n-1;i;i--)
		if(sum+a[i]<=ans)sum+=a[i];
		else ++person,r[person]=i,sum=a[i];
	
	for(int i=person;i;i--)
		cout<<r[i+1]+1<<" "<<r[i]<<endl;
   return 0;
}

3.P1542 包裹快递

由于 double 精度不够，本题卡精度，使用 long double

#include<bits/stdc++.h>
using namespace std;
const double eps=1e-8;
const int N=2e5+10;
int x[N],y[N],s[N],n;
int cal(long double v)    //按照v的速度，求能送几个包裹 
{
	int cnt=0;       //送达包裹数量 
	long double last=0;   //上一个包裹送达后，出发的时间
	
	for(int i=1;i<=n;i++)
	{
		long double t=last+s[i]/v;
		if(t<x[i])cnt++,last=x[i];
		else if(t<=y[i])cnt++,last=t;
		else return i-1;
	}
	return n;	
}
int main()
{
	//ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>x[i]>>y[i]>>s[i];
	
	long double ans=0;
	for(double i=1e9;i>eps;i=i/2)
		if(cal(ans+i)<n)ans+=i;
	
	printf("%0.2Lf",ans);

   return 0;
}

P1083 [NOIP2012 提高组] 借教室

#include<bits/stdc++.h>
#define int long long
const int N=1e6+10;
int n,m,s[N],t[N],d[N],r[N];
int a[N],b[N];
using namespace std;
bool check(int x)
{
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
	for(int i=1;i<=x;i++)
		b[s[i]]+=d[i],b[t[i]+1]-=d[i];
	for(int i=1;i<=n;i++)
	{
		a[i]=a[i-1]+b[i];
		if(a[i]>r[i])return false;
	}
	return true;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>r[i];
	for(int i=1;i<=m;i++)cin>>d[i]>>s[i]>>t[i];
	
	int ans=0;
	for(int i=1<<20;i;i>>=1)
		if(ans+i<=m&&check(ans+i))ans+=i;
	
	if(ans==m)cout<<0;
	else cout<<-1<<endl<<ans+1;
   return 0;
}