#edu1008. 广度优先搜索

广度优先搜索

广度优先搜索 BFS(Breadth First Search) 也称为宽度优先搜索，它是一种暴力访问所有连通节点的算法。 在广度优先搜索算法中，扩展节点是一种树的形态（搜索树），起点就是树根，然后依次访问下一层，最终扩展到全部能到达的节点。每一层中有多个节点，需要把本层中所有节点访问完，再访问下一层，这就需要暂时存下本层刚刚访问到下层节点，而且最早访问到的依然要最早被处理，这就需要一种先到先处理结构，很明显数组就可以做到，从一边进入从另外一边出，就如同排队一样先到先处理 FIFO(First In First Out)。

HyErzd.png

注：根据习惯，队首指针指向队列中真实元素前一个位置，这样做当 head==tailhead==tail 时判断队列为空。

（1）出队：

	++head;       //指针后移  
	u=que[head];  //取出队首节点，存入u中

（2）入队：

	++tail;       //指针后移  
	que[tail]=v;  //将v存入队列末尾

对于某一个节点，需要访问它的所有邻居，但是邻居中可能已经被访问了，如果沿着已经被访问的邻居继续，就会出现循环访问（会出现死循环，想想为什么？），为了避免不再访问已经访问过的节点，也就是判重，可以使用标记数组的方法。部分问题判重比较麻烦，由于节点状态比较离散或者比较复杂，可以使用 map 或者 Hash 函数判重。 伪代码描述算法如下：

版本一：使用数组做队列

1.	BFS( )  
2.	{  
3.	   Template que[N];            //定义Template数组作为队列；  
4.	   int head=0,tail=1;          //队列首指针head=0; 尾指针tail=1；  
5.	   que[tail]=起点;             //初始化队列，将起点存入  
6.	   标记起点被访问  
7.	   while( head < tail )        //队列不为空  
8.	     {  
9.	        u=que[++head];          //出队，指针head后移一位，指向待扩展结点；  
10.	        for ( u 的所有邻居 v )   //枚举u的所有邻居，也就是下一个子节点  
11.	           {   
12.	              if (子节点v符合条件)  //v未访问过  
13.	                {  
14.	                   if (新结点是目标结点) 输出并退出；  
15.	                   que[++tail]=v;   //入队，tail指针后移，然后存入  
16.	                   标记v已经被访问  
17.	                }  
18.	           }  
19.	      }                         
20.	}

版本二：使用STL队列

1.	BFS()  
2.	{  
3.	    queue<Template> Q;     //定义Template类型队列  
4.	    Q.push(初始状态);      //初始化,初始状态存入队列  
5.	    while(!Q.empty())      //队列不空   
6.	    {  
7.	        Template u=Q.front(); //取出队首   
8.	        Q.pop();           //出队  
9.	        for(从u出发枚举所有可达状态v) //找到u的所有可达状态  
10.	            if(v是合法的)    //v需要满足某些条件，如未访问过、未在队内等  
11.	                Q.push(v);   //入队（同时可能需要维护某些必要信息）   
12.	    }    
13.	}

典型模型

模型1. 无权图上两点之间的最短路。给定一个无权图（如下图），求从起点到终点的最短距离，并输出一条路径。

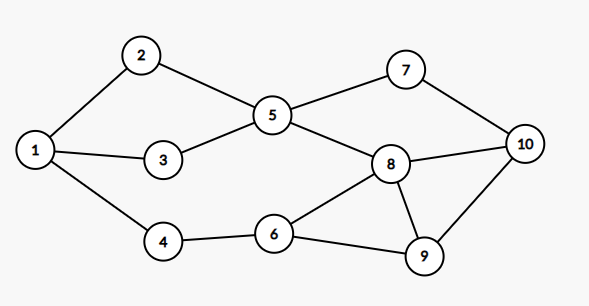
HyUKj1.png

【思路点拨】

BFS 的基本原理就是从起点出发，逐层访问，而每访问一层，实际相当于从起点多往前走了一步。从 A 出发，B、F、D、C是访问的第一层，也就是相当于一步都到，然后会访问H、G、E，也就是往前走两步。 如何存图？可以使用邻接矩阵，F[i][j]=1/0 ,表示 i 与 j 之间存在一条边，但是这种方式复杂度比较高。可以采用邻接表，使用动态数组，第 i 行存 i 个节点的所有邻居。

1.	vector< int >F[N];  
2.	F[i].push_back(v);  //v是i的邻居  
3.	  
4.	//访问i的所有邻居  
5.	for(int j=0;j<F[i].size();j++)     
6.	  {  
7.	     v=F[i][j];   //v就是i的邻居  
8.	     ...  
9.	  }

如何判断是否访问过？可以使用一个标记数组，vis[i]=0/1,表示 i 是否被访问过。 如何输出路径？访问的时候，记录每一个点的前驱节点， pre[i] 表示 i 的前驱节点，递归输出从起点到终点的路径。

参考代码：点击

模型2. 假设有一个网格迷宫，有 nn 行 mm 列的单元格组成，每个单元格要么是空地（用 11 来表示），要么是障碍物（用 00 来表示）。如何找到从起点到终点的最短路径？

【思路点拨】

利用 BFSBFS 就可以直接求解这种隐式无权图的最短路。 如何快速枚举从坐标 (x，y)(x，y) 到上下左右？可以利用方向数组

dx[4]={0,0,1,-1}
dy[4]={1,-1,0,0}
for(int i=0;i<4;i++)
{
int u=x+dx[i];
int v=y+dy[i];
...
}

想一想，如果可以斜着走，或者马走日，如何修改？

坐标是两个数如何放入队列？可以定义两个队列同时操作，也可以定义成结构体，或者使用 pair<int ,int >。

例1. P1144 最短路计数

给出一个 NN 个顶点 MM 条边的无向无权图，顶点编号为1…N1\dots N。问从顶点 11 开始，到其他每个点的最短路有几条。

【思路点拨】

无权图可以利用 BFS 求最短路，可以记录从起点到各点的最短距离，第一次访问到的就是最短距离，如果是第二次访问到而且距离与最短距离相同，那么到这个点的路径条数就应该增加，增加的是上一个点的条数。

1.	#include<bits/stdc++.h>  
2.	using namespace std;  
3.	const int N=1e6+10;  
4.	const int Mod=100003;  
5.	vector<int>f[N];  
6.	int n,m;  
7.	int dis[N],num[N];  
8.	bool vis[N];  
9.	queue<int>que;  
10.	  
11.	void bfs(int i)  
12.	{  
13.	    que.push(i);  
14.	    vis[i]=1; num[i]=1;  
15.	    dis[i]=0;  
16.	    while(que.size())  
17.	    {  
18.	        int x=que.front();  
19.	        que.pop();  
20.	        for(int j=0;j<f[x].size();j++)  
21.	        {  
22.	            int y=f[x][j];  
23.	              
24.	            if(vis[y]==0)  
25.	            {  
26.	                vis[y]=1;  
27.	                que.push(y);  
28.	                num[y]=num[x];  
29.	                dis[y]=dis[x]+1;  
30.	            }  
31.	            else if(vis[y]==1 && dis[x]+1==dis[y])  //再次访问且是最短距离
32.	                num[y]=(num[y]+num[x])%Mod;  
33.	        }  
34.	    }  
35.	}  
36.	int main()  
37.	{  
38.	    scanf("%d%d",&n,&m);  
39.	    for(int i=1;i<=m;i++)  
40.	    {  
41.	        int x,y;  
42.	        scanf("%d%d",&x,&y);  
43.	        if(x!=y)  
44.	        {  
45.	            f[x].push_back(y);  
46.	            f[y].push_back(x);    
47.	        }  
48.	    }  
49.	          
50.	    bfs(1);  
51.	    for(int i=1;i<=n;i++)  
52.	        cout<<num[i]<<endl;  
53.	    return 0;     
54.	}

例2. P2296 [NOIP2014 提高组] 寻找道路

在有向图 G 中，每条边的长度均为 1，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1.路径上的所有点的出边所指向的点都直接或间接与终点连通。

2.在满足条件1的情况下使路径最短。

注意：图 G 中可能存在重边和自环，题目保证终点没有出边。 请你输出符合条件的路径的长度。

【思路点拨】

要满足条件1、2，可以建立一个方向图，如果从终点开始广搜，计算终点达到各点的入边数量，如果等于原图中出边数量，那么就符合题意。可以做两次广搜，第一次在反图上计算终点到达各点入边的数量，第二次在反图上，广搜满足原图出边的数量等于在反图终点到达入边的点。

参考代码：点击

例3. P2658 汽车拉力比赛

博艾市将要举行一场汽车拉力比赛。

赛场凹凸不平，所以被描述为 M∗NM*N 的网格来表示海拔高度 (1≤M,N≤500)(1≤ M,N ≤500) ，每个单元格的海拔范围在 00 到 10910^9 之间。

其中一些单元格被定义为路标。组织者希望给整个路线指定一个难度系数 DD ，这样参赛选手从任一路标到达别的路标所经过的路径上相邻单元格的海拔高度差不会大于 DD 。也就是说这个难度系数 DD 指的是保证所有路标相互可达的最小值。任一单元格和其东西南北四个方向上的单元格都是相邻的。

【思路点拨】

根据题意，难度系数增加，从某路标出发能够到达的路标数量也增加，也就是存在单调性。利用单调性，二分难度系数，对于某一个难度系数，利用广搜计算能够到达路标的数量，求最小的难度系数（达到路标的数量符合题意）就可以了。

参考代码：点击

例4. P2346 四子连棋

在一个 4∗44*4 的棋盘上摆放了 1414 颗棋子，其中有 77 颗白色棋子，77 颗黑色棋子，有两个空白地带，任何一颗黑白棋子都可以向上下左右四个方向移动到相邻的空格，这叫行棋一步，黑白双方交替走棋，任意一方可以先走，如果某个时刻使得任意一种颜色的棋子形成四个一线（包括斜线），这样的状态为目标棋局。

● ○ ●
○ ● ○ ●
● ○ ● ○
○ ● ○

一个4*4的初始棋局，用最少的步数移动到目标棋局的步数。

【思路点拨】

棋盘整体就是一个状态，4∗44*4 保存成一行字符串，有空格的地方可以与上下左右交换，每一次交换都会产生新的状态，新状态如果是目标状态，那就输出交换的次数。

保存成一行，经过上下左右交换，如何得到新状态？ HyEOoT.png

位置 ii，对应的 4∗44*4 棋盘的坐标就是 ((i−1)/4+1，(i−1)( (i-1)/4+1 ，(i-1)%4+1 )，下标都是从 11 开始的，那么上下左右交换的位置也知道了。

想一想如果下标都从 00 开始，其对应坐标如何表示？

如何保证黑白子交替？就某一种状态而言，本次移动黑子或白子，下一层要相反处理，那本步移动了黑子或白子这个状态也需要保存，同时需要保存最少步数，可以使用结构体或者打包成 pair<string ,int>。

如何判断某种状态已经出现过（也就是判重）？可以使用字符串 hash 或者利用 map<string,bool> 进行判重。

参考代码：点击

例5. P1379 八数码难题

在 3×33×3 的棋盘上，摆有八个棋子，每个棋子上标有 11 至 88 的某一数字。棋盘中留有一个空格，空格用 00 来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为 123804765123804765），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

【思路点拨】

3*3 的表格是搜索的状态，拉伸为一维，用 string 表示。 如何判重，是本题重点，可以使用字符串 hash 或者康拓展开判重。

参考代码：点击

反思BFS可以解决什么样的问题？？？

提示：

  1. 边权为 11 的图的最短路问题，如求最短路长度、输出一条最短路径、最短路条数；

  2. 连通性问题，如求连通块大小、连通块个数、判断两个点是否连通；

  1. 关于
  2. 联系我们
  3. Language
  4. 兼容模式
  5. 主题
  3. Worker 0 in 45ms
  4. Powered by Hydro v4.19.1 Modified by byx QQ465039728
  5. 陕ICP备2023000766号