动态规划-区间DP

区间类动态规划是线性动态规划的扩展，用一段区间（左右端点）描述问题，以“区间”作为DP的阶段。在区间DP中，一个状态由若干个比它更小且包含于它的区间所代表的状态转移而来，区间DP的决策往往就是划分区间的方法。

区间类动态规划的特点：将两个或多个部分进行整合，当然也可以反过来，也就是对一个问题分成两个或多个部分。如果能将问题分解成两两合并的形式，是能够用区间dp的特征。

区间DP的解法较为固定，即枚举区间长度，再枚举左端点，之后枚举区间的断点进行转移。

一般情况，令状态 $f(i,j)$ 表示将下标位置 $i$ 到 $j$ 的所有元素合并能获得的价值的最大值，那么 $f(i,j)=max \{ f(i,k)+f(k+1,j)+cost \}$，$cost$ 表示将两段区间合并起来的代价。转移时，必须先合并小区间，再合并大区间，所以首先枚举区间长度。

一般情况下伪代码如下：

for(int i=1;i<=n;i++)f[i][i]=区间长度为1的值; 
    for(int len=2;len<=n;len++)
        for(int i=1;i<=n;i++)
            {
                int j=i+len-1;
                if(j>n)continue;
                for(int k=i;k<j;k++)
                f[i][j]=max/min(f[i][j],f[i][k]+f[k+1][j]+cost);
            }

典型例题：

例1：P1880[NOI1995]石子合并

1. 首先考虑不在环上，只考虑一条链上的情况。

若 $f(i,j)$ 表示区间 $[i,j]$ 内所有石子合并到一起的最大得分。

可得到状态转移方程如下： $f(i,j)=max\{f(i,k)+f(k+1,j)+\sum_{x=i}^{j}a_x \}(i≤k<j)$

显然可以利用全缀和优化区间和 $\sum_{x=i}^{j}a_x$，令 $sum_i$ 表示 $a$ 数组的前缀和，状态转移方程就成为 $f(i,j)=max\{f(i,k)+f(k+1,j)+sum_j-sum_{i-1}\}(i≤k<j)$

2. 怎样进行状态转移？

计算 $f(i,j)$ 的值必须先计算完 $f(i,k)$ 和 $f(k+1,j)$ 的值，也就是先算小区间再算大区间，直接从小到大枚举 $i$ 和 $j$，肯定出错。例如 计算 $f(1,5)$ 时，转移时需要 $f(1,2)+f(3,5)$，$f(3,5)$ 前面没有算过，也就是用未算过的去计算当前状态的值，转移顺序出错。

当然 $i$ 从大到小， $j$ 从 $i+1$ 到大，这种转移顺序也是对的，想想为什么？

不过为了好理解，区间 $dp$ 一般情况下先合并小区间，再合并大区间，所以我们首先从小到大枚举区间长度 $len$,然后枚举 $i$ 的值，根据 $len$ 和 $i$ 用公式计算出 $j$ 的值，然后枚举 $k$，时间复杂度为 $O(n^3)$.

3. 怎样处理环？

题目中是一个环，不是一条链，如何处理？

方法一：石子围成一个环，我们可以枚举分开的位置，将这个环转化为一个链，由于要枚举 $n$ 次，时间复杂度为 $O(n^4)$ 。

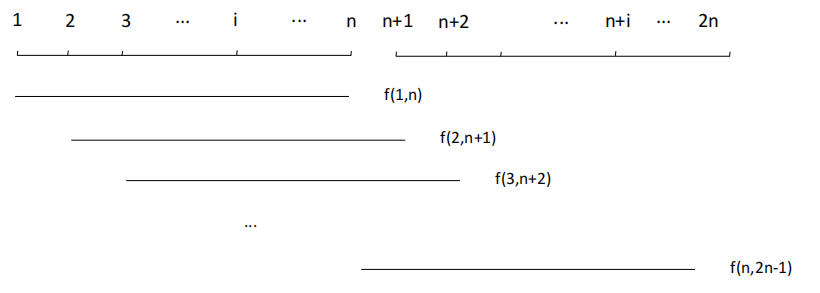
方法二：将这 $n$ 堆石子复制一遍，变成 $2 n$ 堆，也就是复制一遍，破环为链。其中第 $i$ 堆与第 $n+i$ 堆相同，用动态规划求解后，取 $f(1,n),f(2,n+1),...,f(i,n+i-1)$ 中的最优值，即为最后的答案，时间复杂度 $O(n^3)$ .如下图：

参考代码：

#include<bits/stdc++.h>
using namespace std;
int n;
int a[201],sum[201];   //石子的数量，前缀和
int dpmin[201][201],dpmax[201][201] ;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	   {
	   	scanf("%d",&a[i]);
	   	a[i+n]=a[i];
	   }
	sum[1]=a[1];
	for(int i=2;i<=2*n;i++)
	   sum[i]=sum[i-1]+a[i];
	
	memset(dpmin,0x3f,sizeof(dpmin));
	memset(dpmax,-1,sizeof(dpmax));
	
	for(int i=1;i<=2*n;i++)
	  dpmin[i][i]=dpmax[i][i]=0;
	//i从大到小枚举，这样转移也正确？ 想想为什么 
	/*for(int i=2*n;i>=1;i--)          //必须从大到小扩展 
	   for(int j=i+1;j<=2*n;j++)   
	      for(int k=i;k<j;k++)
	        {
	        	dpmin[i][j]=min(dpmin[i][j],dpmin[i][k]+dpmin[k+1][j]+sum[j]-sum[i-1]);
	        	dpmax[i][j]=max(dpmax[i][j],dpmax[i][k]+dpmax[k+1][j]+sum[j]-sum[i-1]);
			}*/
	for(int len=2;len<=n;len++) 
		for(int i=1;i<=2*n;i++)
		{
			int j=i+len-1;
			if(j>2*n)continue;
			for(int k=i;k<j;k++)
				{
	        		dpmin[i][j]=min(dpmin[i][j],dpmin[i][k]+dpmin[k+1][j]+sum[j]-sum[i-1]);
	        		dpmax[i][j]=max(dpmax[i][j],dpmax[i][k]+dpmax[k+1][j]+sum[j]-sum[i-1]);
				}
		}
	
	int ansmin=0x3f3f3f3f,ansmax=-1; 
	for(int i=1;i<=n;i++)   
	{
		ansmin=min(ansmin,dpmin[i][i+n-1]);
		ansmax=max(ansmax,dpmax[i][i+n-1]);
	  }  
	cout<<ansmin<<endl<<ansmax;
	return 0;
}

例2： P1063能量项链

明显的特征，区间具备合并性。环状结构，复制一遍，破环为链。

定义状态 $f(i,j)$ 表示区间 $（i,j）$ 合并后的最大得分， $a[i].l$ 和 $a[i].r$ 表示能量珠$i$的头标记和尾标记。

$$f(i,j)=max(f(i,j),f(i,k)+f(k+1，j)+a[i].l*a[k].r*a[j].r $$

参考代码：点击

例4： P4342 [IOI1998]Polygon

本题与石子合并属于同类问题，经典的区间 $dp$，复制一遍破环为链,但是合并时有区别，对于 $+$，完全相同，但是对于 $*$，可能出现负数，负负为正，小的可能会变成大的，这是本题状态转移时的难点。

$f(i,j)$ 表示合并区间 $(i,j)$ 的最大值，$g(i,j)$ 表示最小值。

当连接符是 $+$ 时，

$f[i][j]=max(f[i][j],f[i][k]+f[k+1][j])$

$g[i][j]=min(g[i][j],g[i][k]+g[k+1][j])$

当连接符是*时，细致讨论过于麻烦，各种情况取最值就可以了：

最大值：

$f[i][j]=max(f[i][j],f[i][k]*f[k+1][j])$

$f[i][j]=max(f[i][j],g[i][k]*g[k+1][j])$

$f[i][j]=max(f[i][j],f[i][k]*g[k+1][j])$

$f[i][j]=max(f[i][j],g[i][k]*f[k+1][j])$

最小值：

$g[i][j]=min(g[i][j],g[i][k]*g[k+1][j])$

$g[i][j]=min(g[i][j],f[i][k]*f[k+1][j])$

$g[i][j]=min(g[i][j],g[i][k]*f[k+1][j])$

$g[i][j]=min(g[i][j],f[i][k]*g[k+1][j])$

参考代码：点击

例5： P1040[NOIP2003 提高组] 加分二叉树

中序遍历 $(1,2,..,i,..n)$ 选择 $i$ 作为树根， $(1,..,i-1)$ 是左子树， $(i+1...,n)$ 是右子树，显然具备区间合并的特性。

定义状态 $f(i,j)$ 表示区间 $(i,j)$ 构成的二叉树得分最大，选择区间中 $k$ 作为树根，可以得到状态转移方程：

$f(i,j)=max(f(i,j),f(i,k-1)*f(k+1,j)+a[k])$

同时记录 区间 $[i,j]$ 取最大值时对应的树根，然后递归前序遍历就是答案，可以使用递推或记忆化搜索实现。

参考代码：点击

例6： P4170[CQOI2007]涂色

本题依然需要用区间描述问题，那么定义 $f(i,j)$ 表示将原区间染成 $s(i,j)$ 需要的最小次数。

根据题意一次能染一段，对于区间$(i,j)$无论颜色怎样，都可以把原来区间$(i,j)$按照$s[i]$或$s[j]$来染，那么$f(i,j)=min(f[i+1][j]+1,f[i][j-1]+1)$。当$s[i]=s[j]$时，可以一次性染成$s[i]$,然后只对$（i+1,j-1）$再染就可以了，也就是$f(i,j)=min(f[i][j],f(i+1,j-1)+1)$。

之前题解受 CF1114D 影响，本题需要枚举中间分割点，以确定最小值。

当 $s[i]=s[j]$ 时，在染区间 $[i+1,j]$ 或 $[i,j-1]$ 只需要多染一格就可以了，于是就有 $f[i][j]=min(f[i+1,j],f[i,j-1])$;

当 $s[i]\ne s[j]$ 时，需要将 $[i,j]$ 分割成 $2$ 个区间进行染色，枚举断点位置 $k$，分别染区间 $[i,k]$ 和 $[k+1,j]$ ，那么 $f[i][j]=min(f[i][k]+f[k+1][j])$

起点： $f[i][i]=1$

状态转移方程：

当 $i<j,s[i]=s[j]$时，$f[i][j]=min(f[i+1][j],f[i][j-1])$ ;

当 $i<j,s[i]\ne s[j]$时，$f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]),i \leq k < j$ ;

参考代码：点击

类似题目：CF1114D Flood Fill

• 题意： 可以将一段颜色一样的区间，通过一次染色染成其他颜色，询问给定 $n$ 种初始颜色，需要最少几次将区间颜色染成一种颜色。

设 $f[i][j]$ 表示将区间 $[i,j]$ 染成一种颜色最少需要的次数；

如果枚举断点 $k$，将区间分两段染色，时间复杂度就是 $O(n^3)$,$n=5000$ 会 $TLE$ ;

本题不需要枚举断点，对于区间 $[l,r]$，有两种决策：

• 1.枚举断点位置 $k$

• 2.只考虑前后端点

决策 1 是包含决策 2 的，本题贪心有效(即：枚举断点 $k$，并不会更优)，详细证明参考讨论：关于不需枚举断点的证明

只考虑前后端点，核心代码：

f[i][j]=min(f[i+1][j]+1,f[i][j-1]+1);
if(c[i]==c[i+1])f[i][j]=min(f[i][j],f[i+1][j]);
if(c[j-1]==c[j])f[i][j]=min(f[i][j],f[i][j-1]);
if(c[i]==c[j]&&i+1<=j-1)f[i][j]=min(f[i][j],f[i+1][j-1]+1);

例7： P1220 关路灯

将一个区间 $(i,j)$ 内的灯全部关闭，根据题意最后关掉的是 $i$ 或者$j$ ，也就是先要关闭掉区间 $(i+1,j)$ 或者 $(i,j-1)$ ，然后再去关闭 $i$ 或者 $j$ ，要用区间描述问题状态，但是自由区间左右端点显然无法表示完整信息，例如要关闭 $i$ ，那么他从 $(i+1,j)$ 区间去关闭，老张站在 $(i+1,j)$ 的左边还是右边了？

为了清楚表达，需要描述关闭完后老张是站在区间左端点还是右端点的,也就是 $(i,j,0/1)$ 描述问题。

$f(i,j,0/1)$ 表示关闭区间 $(i,j)$ 的灯这段时间整个电路电能的最小消耗，$0$ 表示最后停在左端点，$1$ 表示右端点。

在关闭灯 $i$ 这段时间的消耗 $=$ 区间 $(1，i)$ 和 $(j+1,n)$ 的功率和 $*$ 从 $i+1$ 或 $j$ 走到 $i$ 的时间，功率和可以用区间和优化。 $sum[i]$ 表示 $1\dots i$ 的功率和，$a[i]$ 表示距离。

$$f(i,j,0)=min\left\{\begin{matrix} f(i+1,j,0)+(sum[i]+sum[n]-sum[j])*(a[i+1]-a[i]) \\f(i+1,j,1)+(sum[i]+sum[n]-sum[j])*(a[j]-a[i]) \end{matrix}\right. $$

在关闭灯 j 这段时间的消耗= 区间$(1,i-1)$ 和 $(j,n)$ 的功率和$*$ 从 $i$ 或 $j-1$ 走到 $i$ 的时间，功率和可以用区间和优化。

$$f(i,j,1)=min\left\{\begin{matrix}(f(i,j-1,0)+(sum[i-1]+sum[n]-sum[j-1])*(a[j]-a[i]) \\f(i,j-1,1)+(sum[i-1]+sum[n]-sum[j-1])*(a[j]-a[j-1])) \end{matrix}\right. $$

参考代码：点击

类似题目：P2466 [SDOI2008] Sue 的小球 注意同时维护时间的贪心式做法是不对的，想想为什么？（时间并不同步）

本题可以采用"关路灯"的思路，定义 $f[l][r][0/1]$ 接住 $[l,r]$ 所有彩球所有彩球 $y$ 的最小消耗，所有 $y$ 之和 $-min(f[1][n][0],f[1][n][1])$ 就是 $ans$ ,即 $ans=\{\sum{y_i}\}-min(f[1][n][0],f[1][n][1]))$ .

为了保证精度，计算过程使用整数，最终答案需要除以 $1000.0$

升级题目：P4870 [BalticOI 2009 Day1] 甲虫 水滴不能为减少为负数，如何处理？ 依然当成可以减少为负数进行处理，发现喝到的水滴数越多，后面的水滴就会变为负数，答案反而变小，变小的原因就是水滴蒸发完后变为负数。那么我们枚举区间喝到水滴的数量，保留喝到最多的水，最多的水就是答案。

例8： P3205 [HNOI2010]合唱队

根据题意描述问题依然是区间， $f(i,j)$ 表示构成区间 $(i,j)$ 的方法数，转移时最后进入队伍的是 $i$ 还是 $j$，显然需要增加信息， $f(i,j,0/1)$ 表示构成区间 $(i,j)$ 的方法数，$0$ 表示最后 $i$ 进入队伍，$1$ 表示 $j$ 进入队伍。

$f[i][j][0]$ 表示 $i$ 最后进入队伍构成的方法数，当 $h[i]<h[i+1]$时，$f[i][j][0]+=f[i+1][j][0]$，当$h[i]<h[j]$时，$f[i][j][0]+=f[i+1][j][1]$。

$f[i][j][1]$ 表示 $j$ 最后进入队伍构成的方法数，当 $h[j]>h[j-1]$ 时，$f[i][j][1]+=f[i][j-1][1]$，当 $h[j]>h[i]$ 时， $f[i][j][1]+=f[i][j-1][0]$。

参考代码：点击

例9： CF607B Zuma

每次移走一个回文串，用 $f(i,j)$ 表示移走区间 $[i,j]$ 的最小时间。

$f(i,j)=min(f(i,j),f(i,k)+f(k+1,j))$

当 $c[i]==c[j]$ 时， $f[i][j]=min(f[i][j],f[i+1][j-1])$。

本题难点在于起点的确定， 区间长度为 $1$ 时， $f[i][i]=1$；

区间长度为 $2$ 时，当 $c[i]==c[i+1]$ , $f[i][i+1]=1$， 否则 $f[i][i+1]=2$;

参考代码：点击

例10： P2890 [USACO07OPEN]Cheapest Palindrome G

$f(i,j)$ 表示区间 $(i,j)$ 变成回文串的最小花费。区间 $(i,j)$ 可以由 $(i+1,j)$ 删除 $s[i]$ ,或者在$s[j]$ 后增加 $s[i]$ ,得到回文，也可以由区间 $(i,j-1)$ 删除 $s[j]$,或者在 $s[i]$ 前添加$s[j]$ 。

状态转移方程： $f(i,j)=min(f(i+1,j)+del[s[i]],f(i+1,j)+add[s[i]])$; $f(i,j)=min(f(i,j-1)+del[s[j]],f(i,j-1)+add(s[j]))$;

当 $s[i]=s[j]$ 时， $f[i][j]=min(f[i][j],f[i-1][j-1])$;

参考代码：点击

---

学习完毕

{{ select(1) }}

• YES
• NO