树的直径

【树的直径(最远点对)】

给定一颗 $n$ 个结点的边带权的树，找到一条最长的路径。树的直径可能有很多条。

性质：

（1）若有多条直径，则所有的直径之间皆有公共点，树的所有直径拥有相同的中点。

（2）直径的两个端点一定是叶子。(边权是正的情况)

（3）对于两棵树，如果第一棵树直径两端点为 $(u,v)$ ，第二棵树直径两端点为 $(x,y)$ ，用条边将两棵树连接，那么新树的直径一定是 $u,v,x,y$ 中的两个点。(边权是正的情况)

（4）对树上任意一个点，与之距离最远的每一个点，至少有一个直径的端点。（(边权是正的情况)）

解法一：

当树中所有边权都是正数，通过两次遍历找到树的一条直径，本质上就是贪心找到最远点对。

第一次遍历，找到距离某个结点（例如根结点）最远的一个点 $x$

第二次遍历，找出距离结点 $x$ 最远的一个点 $y$

$x$ 到 $y$ 的简单路径，即为树的一条直径。

为了找到距离某个点最远的点，这颗树应该看作无根树，一个结点连向父亲的边也要存入邻接表中。

注意： 这种方法是基于贪心的，对于图中存在负边，这种方法是错误的，为什么？ (遍历的话始终要走到叶子节点，而当边权为负，直径两端点就不一定是叶子。另外在这种情况下，从任意起点出发，不一定能够到达直径的两个端点。)

优点:可以记录直径的起点、终点，再通过找前驱 ( $father$ )，可以访问直径上的边和点。

缺点：无法处理边权为负的树。

参考代码 （深搜的方式）

int x,y,de[N];
void dfs(int u,int fa)
{
    de[u]=de[fa]+1;
    for(int i=head[u];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa)continue;
        dfs(v,u);
    }
} 
void solve()
{
    dfs(1,0);
    x=1;
    for(int i=2;i<=n;i++)if(de[i]>de[x])x=i;
    dfs(x,0);
    y=1;
    for(int i=2;i<=n;i++)if(de[i]>de[y])y=i;
    printf("%d %d\n",x,y);
    printf("%d",de[y]);
 } 

解法二：

树形 $DP$ 求树的直径

设 $1$ 号节点为根，有根树

设 $D[X]$ 表示从节点 $x$ 出发走向以 $x$ 为根的子树，能够到达的最远节点的距离

接下来考虑，经过 $x$ 的最长链的长度 $F[x]$

实际没必要双层循环枚举 $i,j$ 。我们可以思考 $D[x]$ 的计算过程。在子节点的循环将要枚举到 $i$ 时，$D[x]$ 恰好就保存了从节点 $x$ 出发走向“以 $y_j$ 为为根的子树”，能够到达的最远节点的距离，这个距离就是 $max \{ D[y_j]+edge(x,y_j)\}$ 。所以，此时我们先用 $D[x]+D[y_j]+edge(x,y_j)$ 更新 $F[x]$ ，再用 $D[y_j]+edge(x,y_j)$ 更新 $D[x]$ 即可。

$F[x]$ 就是最长链的一个备选答案，可以直接更新答案。

优点:可以处理负边权的树

缺点:只能求出直径的长度。

核心参考代码:

int ans;
void dp(int x)
{
    vis[x]=1;
    for(int i=head[x];i;i=edge[i].next)
    {   int y=edge[i].to;
        if(vis[x])continue;
        dp(y);
        ans=max(ans,d[x]+d[y]+edge[i].dis);
        d[x]=max(d[x],d[y]+edge[i].dis);
    }
}

另一种方式 ：最长链+次长链

int len=0;
int dfs(int x,int fa)   //返回x到叶子结点的最远距离 
{   int first=0,second=0;
    for(int i=head[u];i;i=edge[i].next)
    {
        int y=edge[i].to;
        if(y==fa)continue;
        int temp=dfs(y,x)+edge[i].dis;
        if(temp>first){
            second=first;
            first=temp;
        }else if(temp>second)second=temp;
    }
    len=max(len,first+second);
    return first;
}

另一种版本

int len=0;
int d1[N],d2[N];
//d1[i]表示以i为根的子树中，i到叶子结点的距离最大值
//d2[i]表示以i为根的子树中，i到叶子结点的距离次大值 
int dfs(int x,int fa)   //返回x到叶子结点的最远距离 
{
for(int i=head[u];i;i=edge[i].next)
    {
        int y=edge[i].to;
        if(y==fa)continue;
        int temp=dfs(y,x)+edge[i].dis;
        if(temp>d1[x]){
            d2[x]=d1[x];
            d1[x]=temp
        }else if(temp>d2[x])d2[x]=temp;
    }
    len=max(len,d1[x]+d2[x]);
    return d1[x];
}

例题 P3629 [APIO2010] 巡逻

思路分析：

题目中有特殊要求，$k==1$ 或 $2$,新修的路必须走，那么可以从这两个特殊要求切入。

1. $k==1$

此时只需要修一条路，这条路会与原树上的路径之间形成一个回路，巡逻的时候，就少走原树的路径，那显然原树上路径越长越好，显然就是树的直径 $L1$，最终 $ans=2*(n-1)-L1+1$ 。

2. $k==2$

此时需要修两条路，绘图会发现，两个回路重复的地方还是要走两遍，意味着，第 $2$ 条路并不是越长越好，会受第一条路的影响，即单纯再求一条次长路是错误的，那怎么办？

既然重复的路径还是走两遍，重复的地方对答案没有贡献，那么第一次求完直径后，我们将这条直径上的边权都改为 $-1$ ,这样第二次求直径，如果选择了重复的边，由于边权是 $-1$ ,相当于对答案没有贡献，由于边权是$-1$ ，反而使得我们尽量少选择重复的路，无论如何这种情况，第 $2$ 次求的直径 $L2$ 是节省的最大值，不过第二次求直径，由于边权有负，需要使用动态规划求直径。

基本过程：

(1)两次遍历求出直径 $L1$

(2)将直径上的边权修改为 $-1$

(3)利用 DP 求出修改后直径 $L2$

$ans=2*(n-1)-L1-L2+2=2*n-L1-L2$

参考代码：点击

---

树的重心

定义1：对于 $n$ 个节点的无根树，找到一个点，使得把树变成该点为根树时，最大子树的节点数最小。即删除这个点后最大联通快的节点数最小，那么这个点就是树的重心。

定义2：一颗具有 $n$ 个结点的无根树，若以某个结点为整个树的根，它的每个儿子的子树大小都小于等于 $n/2$，则称这个点为该树的重心。

定义1和2本质是一样的，想想为什么？

树的重心的性质

1.树的重心如果不唯一，则至多有两个，且这两个重心相邻；

2.以树的重心为根时，所有子树的大小都不超过整棵树大小的一半。

3.树中所有点到某个点的距离和中，到重心的距离和是最小的；如果有两个重心，那么到它们的距离和一样。

4.两个树通过一条边合并，新的重心在原树两个重心的路径上；

5.树删除或添加一个叶子节点，重心最多只移动一条边；

如何求重心？？？

方法1：利用定义1

枚举每一个点寻找删除后最小的连通块，删除重心后最大连通块的节点数最小，那么就要对每个结点，以其为根，找出其所有子树的最大节点数，然后找出子树对打结点数最小的那个结点，即是重心。

int size[N],g[N]; 
//size[i]以i为根子树的节点个数
//g[i]以i为根 最大的子树节点的数量 
int p=1;  //p保存根节点
 
for(int i=1;i<=n;i++)
   if(g[p]>g[i])p=i;
// p就是重心 

void dfs(int u,int fa)
{
    size[u]=1;
    for(int i=head[u];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa)continue;
        dfs(v,u);               
        size[u]+=size[v];
        g[u]=max(g[u],size[v]);
    }
    g[u]=max(g[u],n-size[u]);
}

方法2：利用定义2 对于无根树，选择一个节点作为根，求出每个节点为根子树的大小。 然后枚举每一个结点，看看它往下的子树（即以它的每个儿子为根的子树）与往上的子树（即整棵树去除以其为根的子树的部分）的大小是否都小于等于 n/2 。

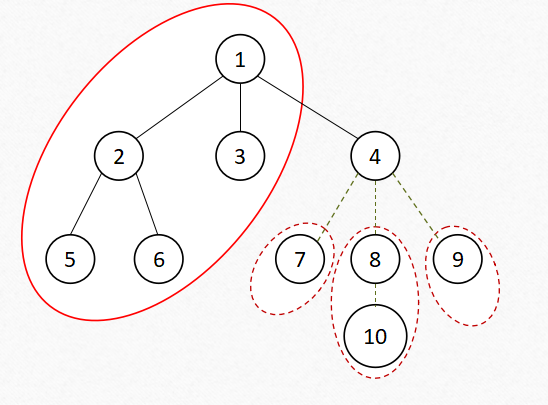
如图，以 $1$ 为根，枚举到 $4$ 号节点,$4$ 号节点为根，虚线框出的部分为向下的子树，实线框出的部分为向上的子树。

参考核心代码

int size[N]，fa[N];  
//size[i] 表示以i为根的子树节点个数
int getsize(int u) //求u为根各个子树的大小 
{
    size[u]=1;
    for(int i=head[u];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa[u])continue;
        fa[v]=u;   //找到v的父亲u 
        size[u]+=getsize(v); 
     } 
    return size[u];
} 
bool check(int u)   //检测 u 是否为树的根
{
    if(n-size[u]>n/2)return 0;
    for(int i=head[u];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa[u])continue; 
        if(size[v]>n/2)return 0;
    }
    return 1;
} 

主函数调用:

getsize(1);
for(int i=1;i<=n;i++)
     if(check(i))
        {        cout<<i是重心; break;   }

CF685B Kay and Snowflake

给定一颗树，求以节点i为根的子树的重心。

分析：如果$x$的子树$y$重心确定了，那么子树$x$的重心一定落在最大的那子树（$size[y]>size[x]/2$）的重心到$x$的路径上，当然如果没有这样的重儿子，那么$x$就是子树$x$的重心，这是由重心定义决定的。

参考代码：点击

---

树的中心

定义： 以树的中心为整棵树的根时，从该根到每个叶子节点的最长路径最短。 树的中心一定在直径上，且最多有两个。

（1）树形$DP$求中心

我们需要维护每个点到所有叶子节点的最长距离

前面已经知道了怎么维护每个节点到它的子树中的叶子节点的最长距离和次长距离，考虑怎么维护这个点向上的最远距离

$c1[i]$表示$d1[i]$从哪个点更新，$c2[i]$表示$d2[i]$从哪个点更新，用$up[i]$表示向上的最远距离。

再用一开始指定的点做一次$DFS$，这次是从根到叶子节点状态转移。

对于每一个点，假设它的父亲的最长链，也就是$d1[fa[u]]$不是从它更新来的，那么$up[u]=max(up[fa[u]],d1[fa[u]])+dis[fa[u]][u]$ 如果的父亲的最长链是从它更新来的，那次长链一定不是从它更新来的，可以看看前面的定义，两条链没有交集，所以 $up[u]=max(up[fa[u]],d2[fa[u]])+dis[fa[u]][u]$

最后这样更新答案:

ans=min(ans,max(up[i],d1[i]));

（2）$DFS/BFS$求中心

树的中心一定在树的直径上，且趋于中点

这个是比较显然的，如果不在直径上，它的最远距离只会更远

因此我们在找出直径的同时，对于直径的两个端点$pos1,pos2$，分别求到每个点的距离$d1[i],d2[i]$

最后对于每个点更新即可

ans=min(ans,max(d1[i],d2[i]));

经典例题：P6419 [COCI2014-2015#1] Kamp

换根维护以每个点为根到其他标记点的距离和(需要走的路径*2，折返)，以及根到最远标记点的距离，答案就是距离和-根到最远标记点的距离。

---

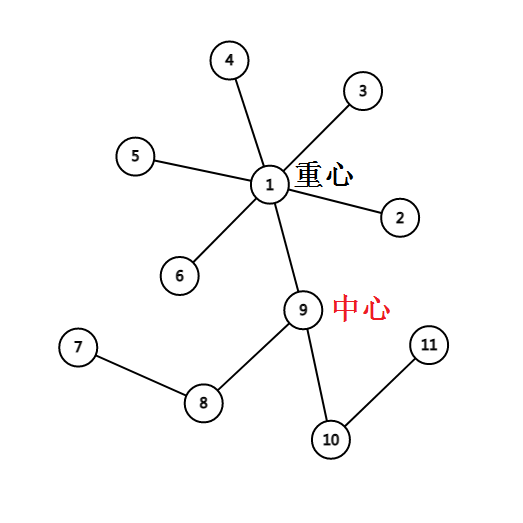
树的重心不一定在直径上，树的中心一定在树的直径上

例如：

考虑一个 n+1 个点的菊花和一条 n 个点的链。

将菊花的根和链的中点连起来构成一棵树。

这棵树的重心是菊花的根，直径是 n 个点的链。

---

学习完毕

{{ select(1) }}

• YES
• NO