线段树综述

树状数组的本质是利用二进制进行区间分块。而对于更一般的区间问题，可以使用额外空间存储整个区间信息，高效率 $O(\log{n})$ 修改、查询区间 $[l,r]$ 的信息，线段树就显示出巨大优势,与树状数组相比更加通用。

• 1.线段树中每个节点代表一段区间；
• 2.唯一的根节点代表整个统计区间，根节点 $1$ 代表区间 $[1,n]$;
• 3.线段树叶子节点代表一个长度为 $1$ 的区间，区间 $[l,r]$ 当 $l==r$ 时区间长度为 $1$ ，到达叶子节点，计算完后要返回；
• 4.对于每个节点所代表的区间 $[l,r]$ ,左节点是 $[l,mid]$ ，右节点是 $[mid+1,r]$ ,其中 $mid=\frac{l+r}{2}= l+r >>1$ (右移运算符优先级低于算术运算符，可以省掉括号)

线段树-区间视图

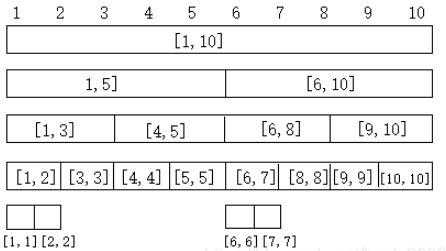
线段树-二叉树视图

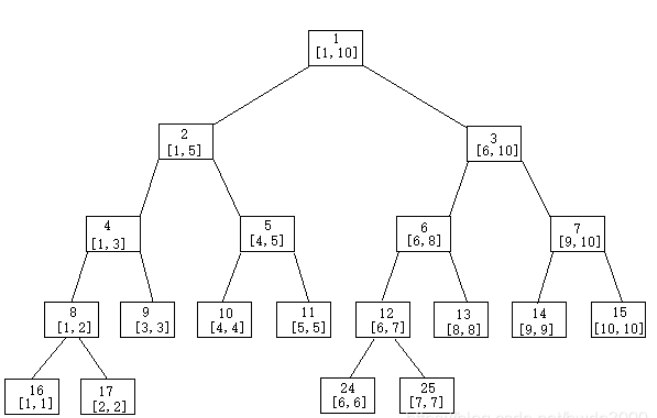
线段树利用类似于二叉堆的方式建立起父亲节点编号与儿子节点编号的关系，即对于编号为 $p$ 的节点左儿子为 $2*p=p<<1$ ,右儿子为 $2*p+1=p<<1|1$ ,父亲节点为 $\frac{p}{2}=p>>1$。

• 整颗线段树一定是一颗完全二叉树，$n$ 个节点完全二叉树深度 $h$ 的取值范围：

$\left \lceil \log_{2}{(n+1)} -1\right \rceil < h \le \left \lceil \log_{2}{(n+1)} \right \rceil $ ，取上限 $h=\left \lfloor \log_{2}{(n)} \right \rfloor +2$,高度为 $h$ 的完全二叉树节点总数不超过 $N \le \sum_{i=0}^{h-1}(2^i)=2^h-1 = 4*n-1$ ， 所以保存线段树数组长度不小于 $4*n$ ,才能保证不会越界。

---

接下来，利用线段树维护区间最大值为例，分析线段树创建、修改、查询。

（1）建树

给定一个长度为 $N$ 的序列 $a$，我们可以创建在区间 $[1,N]$ 上创建一颗线段树，每个叶子节点 $[i,i]$ 保存 $a[i]$ 的值，线段树的二叉树结构很方便从下往上传递信息，即 $data[l,r]=max(data[l,mid],data[mid+1,r])$,也就是 $t[p].data=max(t[2*p].data,t[2*p+1].data)$.

时间复杂度为 $O(n)$

const int N=1e5+10;
int a[N],n;
struct node{
	int l,r;
	int data;
}t[N<<2];   //N<<2 = N*4
void build(int p,int l,int r)
{
	t[p].l=l,t[p].r=r;      //节点p表示区间[l,r]
	if(l==r)             //叶子
	{
		t[p].data=a[l];
		return;
	}
	int mid= l+r >>1;         //mid=(l+r)/2
	build(p<<1,l,mid);        //2*p = p<<1 
	build(p<<1|1,mid+1,r);     //2*p+1 = p<<1|1
	t[p].data=max(t[p<<1].data,t[p<<1|1].data);  //从下往上传回信息
}

build(1,1,n);  //调用入口

（2）单点修改

单点修改就是将 $a[x]$ 加上一个数 $d$.

在线段树中,根节点（编号为 $1$ 的节点）是执行各种指令的入口。我们需要从根节点出发，递归找到区间 $[x,x]$ 也就是叶子节点，修改后，再从下往上更新其祖先节点。执行次数就是整个树的深度，因此时间复杂度为 $O(\log{n})$ .

void change(int p,int x,int d)  // 单点修改 给a[x]加d 
{
	if(t[p].l==t[p].r)
	{
		t[p].data+=d;
		return; 
	}
	int mid=t[p].l+t[p].r >>1;
	if(x<=mid)change(p<<1,x,d);   //x属于左半区间 
	else change(p<<1|1,x,d);     //x属于右半区间 
	t[p].data=max(t[p<<1].data,t[p<<1|1].data); 
}

（3）区间查询

查询区间 $[l,r]$ 的最大值，只需要从根节点的出发，递归执行以下过程：

• 1.如果查询区间 $[l,r]$ 完全覆盖了当前点代表的区间，也就是当前点所代表的信息是询问区间一部分，那直接将当前点 $data$ 返回，作为候选答案。
• 2.如左子树节点与 $[l,r]$ 有重叠部分，则递归访问左子树。
• 3.如右子树节点与 $[l,r]$ 有重叠部分，则递归访问右子树。

int query(int p,int l,int r)
{
	if(l<=t[p].l&&t[p].r<=r)return t[p].data;
	int mid=t[p].l+t[p].r >>1;
	int ans=-(1<<30);
	if(l<=mid)ans=max(ans,query(p<<1,l,r));
	if(mid<r)ans=max(ans,query(p<<1|1,l,r));
	return ans;
}

询问区间 $[l,r]$,那么复杂度是多少？

实际该过程会把询问区间 $[l,r]$ 在线段树上分成 $O(\log{n})$ 个节点，取其最大值作为答案，因此复杂度为 $O(\log{n})$ 。（分情况讨论就可以证明）

（4）区间修改 -lazy 延迟标记

需要对一个区间 $[l,r]$ 进行修改时，如果暴力将区间修改做单点修改，区间修改一次复杂度就为 $O(n\log{n})$ ,$m$ 次修改复杂度无法接受（比单纯数组修改复杂度还大）。

实际上，如果修改区间 $[l,r]$，完全覆盖了节点 $p$ 所代表的区间 $[p_l,p_r]$ ，而在查询的时候查询区间也完全覆盖了节点$p$所代表的区间，我们没必要修改节点 $p$ 以下的所有子树节点，这会做很多无用功。

也就是，在执行修改指令时，同样可以在 $l \le p_l \le p_r \le r$ 情况下立即返回，只不过在回溯之前在节点 $p$ 增加一个标记，标识“该节点曾经被修改，但其子节点尚未被更新。”

但是在查询时，如果需要从节点 $p$ 向下递归，我们再检查$p$是否具有标记。如果有标记，根据标记信息更新 $p$ 的两个子节点，同时为 $p$ 的两个子节点增加标记，然后清除$p$的标记。

也就是说，出了在修改指令中直接划分成 $O(\log{n})$ 个节点之外，对于任意节点修改都延迟到“在后续操作中需要递归其子孙节点时，再修改”，这样每条查询或修改（区间修改）指令时间复杂度都降低到了 $O(\log{n})$,这个标记就是延迟标记。

核心代码：

void pushup(int p)
{
	t[p].sum=t[2*p].sum+t[2*p+1].sum;	
} 
void pushdown(int p)
{
	if(t[p].lazy)
	{
		t[2*p].sum+=t[p].lazy*(t[2*p].r-t[2*p].l+1);  //更新左子树 
		t[2*p+1].sum+=t[p].lazy*(t[2*p+1].r-t[2*p+1].l+1);//更新右子树 
		t[2*p].lazy+=t[p].lazy;   //下传标记 
		t[2*p+1].lazy+=t[p].lazy;
		t[p].lazy=0;              //注意本节点标记清空 
		return ;
	}
}

void change(int p,int l,int r,int d)
{
	if(l<=t[p].l&&t[p].r<=r)
	{
		t[p].sum+=d*(t[p].r-t[p].l+1);
		t[p].lazy+=d;
		return;
	}
	//未执行return 需要进入到子树中
	 
	pushdown(p);     //下传延迟标记 
	int mid=(t[p].l+t[p].r)>>1;
	if(l<=mid)change(2*p,l,r,d);
	if(mid<r)change(2*p+1,l,r,d);
	pushup(p);      //从左右子树更新根节点信息 
}
long long ask(int p,int l,int r)
{
	if(l<=t[p].l&&t[p].r<=r)return t[p].sum;
	//未执行return 说明需要进入到子树中查询 
	pushdown(p);     //下传延迟标记
	int mid=(t[p].l+t[p].r)>>1;
	long long val=0;
	if(l<=mid)val+=ask(2*p,l,r);
	if(mid<r)val+=ask(2*p+1,l,r);
	return val;
}

注意：实际上当给定 $n$ 以后，线段树结构就已经确定了，可以不用单独建树，打比赛为了节省时间，只需要进行修改、查询就可以了, 下面的模版参考代码都只有修改和查询操作。

模板1：单点修改，区间查询

P3374 【模板】树状数组 1

【题意简化】

【分析】单点修改，区间查询，可以用树状数组，也可以使用线段树维护，参考代码：点击

模版2：区间修改，区间查询

P3372 【模板】线段树 1

【题意简化】给定一个长度为 $n(\le 10^5)$ 的序列，$m(\le 10^5)$ 次操作，包括给区间 $[l,r]$ 加 $k$ , 询问 $[l,r]$ 区间和。

【分析】对于区间修改，线段树一个节点被修改区间完全覆盖，利用延迟标记，不再往下递归，由于“任意区间对应线段树上 $O(\log{n})$ 个管理员”，那么修改的时间复杂度就是 $O(\log{n})$。

参考代码：点击

P3373 【模板】线段树 2

【题意简化】区间修改有乘法和加法，询问区间和。

【分析】区间修改有乘法和加法，那么区间懒惰标记要有乘懒惰标记和加懒惰标记。

• 乘法标记初始化为 1 ，加法懒标记初始为 0 。
• 下传标记的时候应该先下传乘法标记，并且乘法标记会修改子树中加法标记(即加法标记也会扩大相应倍数) ，乘法标记清空，应该清空成 1 不是 0。
• 由于乘操作和加操作影响是不一样的，需要写两个修改函数，一个是乘法修改，一个是加法修改。

参考代码：点击

---

例1：SP1716 GSS3 - Can you answer these queries III

题意：给定义长度为 $N$的序列 $A$, $M$ 条指令，"$1$ $x$ $y$" 表示查询区间 $[x,y]$ 中最大连续子段和，"$2$ $x$ $y$" 表示将 $A[x]$ 改成 $y$. （即维护待修改的区间最大子段和）

分析：每个节点除了维护区间端点外，再维护 $4$ 个信息：区间和 $sum$,区间最大连续子段和 $data$，紧靠左端的最大连续子段和 $lmax$，紧靠右端的最大连续子段和 $rmax$。 从下往上更新这 $4$ 个信息：

$t[p].sum=t[2*p].sum+t[2*p+1].sum$

$t[p].lmax=max(t[2*p].lmax,t[2*p].sum+t[2*p+1].lmax)$

$t[p].rmax=max(t[2*p+1].rmax,t[2*p].rmax+t[2*p+1].sum)$

$t[p].data=max(t[2*p].data,t[2*p+1].data,t[2*p].rmax+t[2*p+1].lmax)$

经常我们从下往上更新封装到 $pushup(p)$ 函数中，这样修改程序只需要修改 $pushup$ 函数。

参考代码：点击

双倍经验：P4513小白逛公园

例2：P1558 色板游戏

例3: P4145 上帝造题的七分钟 2 / 花神游历各国

例4: P1712 [NOI2016] 区间

【分析】“线段树+尺取法” 好题。

对于所有区间按照区间长度排序(左端点排序是不正确的)排序，线段树要维护最大值，想到“尺取法”，$l$ 往前移动，$r$ 只能向右移动，满足“尺取法”要求。

$r$ 不断往右移动，每次移动 $r$ 这个区间需要在线段树上区间 $+1$ ,当线段树上最大值为 $m$ 停止，此时 $r$ 对应最大区间，$l$ 对应最短区间，它们的差就是备选答案，答案就是保留最大-最小的最小值。接下来 $l$ 这个区间，在线段树上区间 $-1$，继续重复移动 $r$ 。

例5: P10463 Interval GCD

例6：P1471 方差

---

扫描线

P5490 【模板】扫描线

P1856 [IOI 1998][USACO5.5] 矩形周长 Picture

例7：P1502 窗口的星星

例8：[ABC327F] Apples

---

学习完毕

{{ select(1) }}

• YES
• NO