#edu2030. 【教程】可持久化线段树
【教程】可持久化线段树
使用线段树可以维护区间信息,即“数据集合的最新状态”。如果想知道数据集任意时间的历史状态,如果将每次历史修改单独保存一份,修改 次,会多浪费 的空间,“可持久化”提供了一种思想,在每项操作后,只 ,不拷贝其他部分。
以区间最大值为例,线段树“单点修改”只会使得 个对应的节点更新,如果每个被更新的节点 ,我们创建该节点的副本 ,只要 不是叶子节点,必然会继续修改 的左、右子树之一。
更新节点 会创建副本 ,假如更新了 的左子树,递归进入 左子树 ,对应子树也会创新相应的副本,线段树深度为 ,那么修改一次,从树根到叶子,新产生的节点数也为 ,下面这幅图就展示了副本的产生过程。
1.线段树初始状态
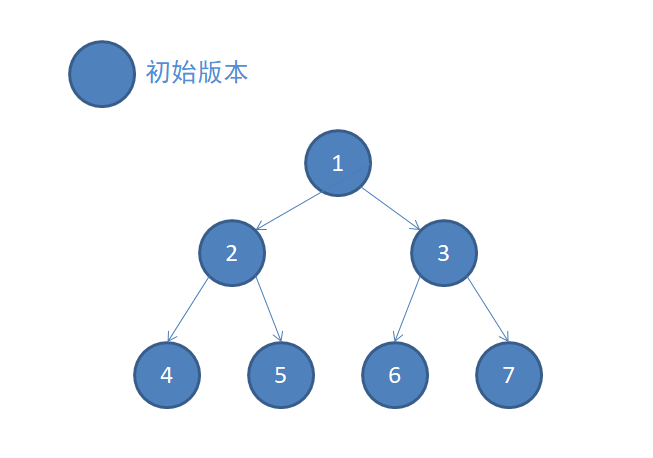
2.在初始版本进行第一次修改,经过的节点都会创造新副本
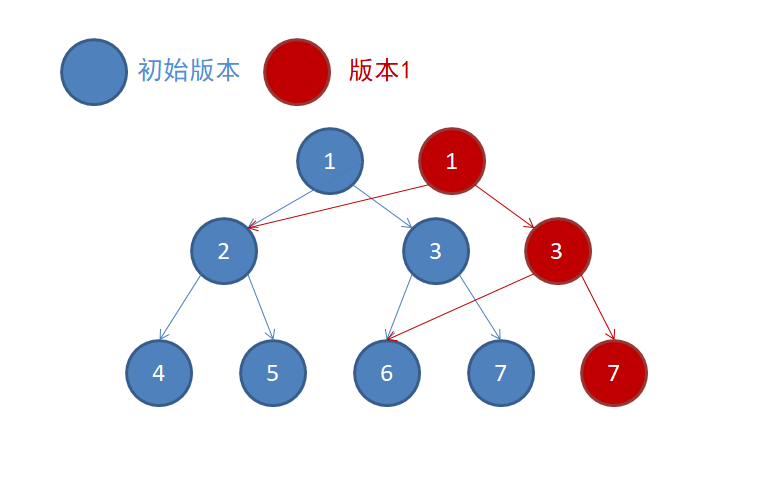
3.第二次修改,会在第一次修改的版本上再创建新副本
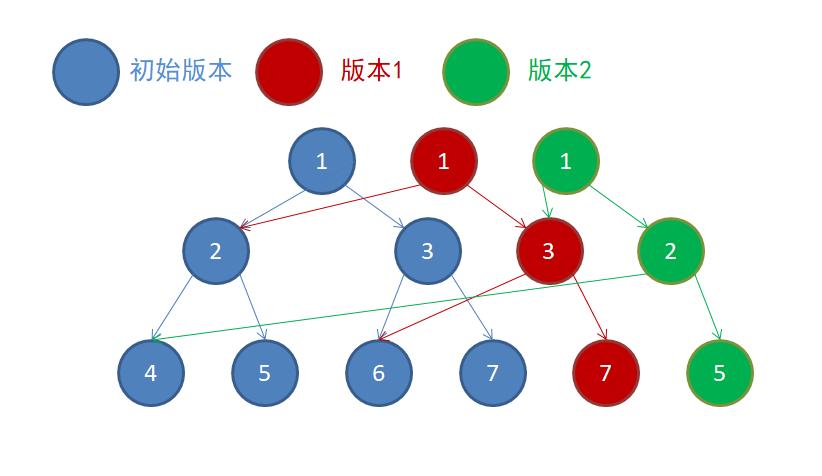
空间复杂度,动态开点线段树会创建 ,每次修改会创建 个新节点, 次修改,创建 , 总空间复杂度为
1.动态开点创建线段树
int n,m,a[MaxN];
struct node{
int ls,rs; //左右儿子编号
int val;
}t[Max(N+M)*Max_logN];
int root[N],tot;//root[i] 版本i的根
int build(int l,int r)
{
int p=++tot;
if(l==r){
t[p].val=a[l];
return p;
}
int mid=l+r>>1;
t[p].ls=build(l,mid);
t[p].rs=build(mid+1,r);
t[p].val=0;
return p;
}
//主函数调用
root[0]=build(1,n);
2.单点修改,a[x] 增加 d ,维护区间最大值
int modify(int now,int l,int r,int x,int d)
{
int p=++tot;
t[p]=t[now];
if(l==r){
t[p].val+=d;
return p;
}
int mid=l+r>>1;
if(x<=mid)t[p].ls=modify(t[now].ls,l,mid,x,d);
else t[p].rs=modify(t[now].rs,mid+1,r,x,d);
t[p].val=max(t[t[p].ls].val,t[t[p].rs].val);
return p;
}
//主函数调用
root[i]=modify(root[i-1],1,n,x,d);
3.区间查询与普通线段树相同。
例1.P3919 【模板】可持久化线段树 1(可持久化数组)
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct node{
int ls,rs;
int val;
}t[N*30];
int n,m,a[N];
int root[N*30],tot;
int build(int l,int r)
{
int p=++tot;
if(l==r)
{
t[p].val=a[l];
return p;
}
int mid=l+r>>1;
t[p].ls=build(l,mid);
t[p].rs=build(mid+1,r);
return p;
}
int modify(int now,int l,int r,int x,int d)
{
int p=++tot;
t[p]=t[now];
if(l==r)
{
t[p].val=d;
return p;
}
int mid=l+r>>1;
if(x<=mid)t[p].ls=modify(t[now].ls,l,mid,x,d);
else t[p].rs=modify(t[now].rs,mid+1,r,x,d);
return p;
}
int query(int p,int l,int r,int x)
{
if(l==r)return t[p].val;
int mid=l+r>>1;
if(x<=mid)return query(t[p].ls,l,mid,x);
else return query(t[p].rs,mid+1,r,x);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",a+i);
root[0]=build(1,n);
for(int i=1;i<=m;i++)
{
int v,op,loc,value;
scanf("%d%d%d",&v,&op,&loc);
if(op==1)
{
scanf("%d",&value);
root[i]=modify(root[v],1,n,loc,value);
}
else
{
int ans=query(root[v],1,n,loc);
printf("%d\n",ans);
root[i]=root[v];
}
}
return 0;
}
例2. P3834 【模板】可持久化线段树 2
静态区间第 小查询
分析:离散化后,从小到大对于每一个 ,在可持久化线段树上在 ( 数组是离散化后数组) 处单点修改 ,此时可持久化线段树中**“以 为根的线段树”的值域区间 和,就保存了 数组前 个数有多少个落在了值域 内**。
查询区间 第 小,有重要性质:以 和 为根的两颗线段树对值域的划分是相同的。两棵线段树的内部对应节点所有代表的值域区间完全相同。
" 的值域区间 的个数 "减去" 的值域区间 的个数 "就等于 有多少个点落在 内,也就是可持久化线段树中两个代表相同值域的节点具有可减性。
查询核心代码:
int query(int p,int q,int l,int r,int k)
{
if(l==r)return l;
int mid=l+r>>1;
int lcnt=t[t[p].ls].val-t[t[q].ls].val; //计算落入[l,mid]区间内的个数
if(k<=lcnt)return query(t[p].ls,t[q].ls,l,mid,k);
else return query(t[p].rs,t[q].rs,mid+1,r,k-lcnt);
}
int ans=query(root[r],root[l-1],1,n,k); //主函数调用
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,m,a[N],b[N],h[N];
struct node{
int ls,rs;
int val;
}t[N*30];
int root[N],tot;
int build(int l,int r)
{
int p=++tot;
if(l==r){
t[p].val=0;
return p;
}
int mid=l+r>>1;
t[p].ls=build(l,mid);
t[p].rs=build(mid+1,r);
t[p].val=0;
return p;
}
int modify(int now,int l,int r,int x,int d)
{
int p=++tot;
t[p]=t[now];
if(l==r){
t[p].val+=d;
return p;
}
int mid=l+r>>1;
if(x<=mid)t[p].ls=modify(t[now].ls,l,mid,x,d);
else t[p].rs=modify(t[now].rs,mid+1,r,x,d);
t[p].val=t[t[p].ls].val+t[t[p].rs].val;
return p;
}
int query(int p,int q,int l,int r,int k)
{
if(l==r)return l;
int mid=l+r>>1;
int lcnt=t[t[p].ls].val-t[t[q].ls].val; //计算落入[l,mid]区间内的个数
if(k<=lcnt)return query(t[p].ls,t[q].ls,l,mid,k);
else return query(t[p].rs,t[q].rs,mid+1,r,k-lcnt);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",a+i);
b[i]=a[i];
}
sort(b+1,b+n+1);
for(int i=1;i<=n;i++)h[i]=lower_bound(b+1,b+n+1,a[i])-b;
root[0]=build(1,n);
for(int i=1;i<=n;i++)
root[i]=modify(root[i-1],1,n,h[i],1);
while(m--)
{
int l,r,k;
scanf("%d%d%d",&l,&r,&k);
int ans=query(root[r],root[l-1],1,n,k);
printf("%d\n",b[ans]);
}
return 0;
}
例1.P3567[POI 2014] KUR-Couriers
【题意】给一个长度为 的正整数序列 。共有 组询问,每次询问一个区间 ,是否存在一个数在 中出现的次数严格大于一半。如果存在,输出这个数,否则输出 .
例2. 区间内不同的个数,强制在线
【分析】之前使用树状数组维护,对于区间内不同的个数,还可以使用主席树维护。
例3. P4137 Rmq Problem / mex
【题意简化】:给定长度为 的数组 。 次询问,每次询问一个区间内最小没有出现过的自然数。
【分析】:以 为下标,维护 最后出现 下标 ,创建可持久化线段树。
在第 棵线段树 上二分,找到最小的、最后一次出现位置在 左侧的数,这个数就是所求的答案。
注意:代码中 val 维护的是这个区间内最后一次出现位置的最小值,而不是第一次出现位置。
参考代码:点击
例4. P2633 Count on a tree
【题意简化】给定一棵 个节点的树,每个点有一个权值。有 个询问,每次给你 ,你需要回答 和 这两个节点间第 小的点权。
例5.P4587 [FJOI2016] 神秘数
【题意简化】对于一个可重复集合,定义神秘数表示集合子集和不能表示的最小的数。 给定长度为 数组 , 次询问,询问区间内集合对应的神秘数。
【分析】
首先我们先分析一个暴力性质: 设集合能表示的数的范围是 , 当 加入时,原来集合表示的范围变为 。如果 , 即两段能够接上,新集合能表示的范围就是 ,否则 无法表示。
可以使用可持久化线段树,维护以 为线段树下标的总和。设 , 循环执行 :在 线段树上去掉 (保证是对应区间 ), 查询小于等于 所有数之和 ,如果 , 说明小于等于 里面有数能够凑出更大的值域范围,此时令 ,否则 就是答案。
参考代码:点击
例6.P7424 [THUPC 2017] 天天爱射击
【题意简化】给定 块木板,木板左右端点为 , 当被子弹击中 次,木板破裂。依次给定 颗子弹,子弹发射位置为 , 询问每颗子弹能够击碎木板的数量。
【分析】本题可以使用整体二分,也可以利用可持久化线段树解决。
我们可以将题意转换为:对于每块木板,当所有子弹发射,最早被哪一颗子弹击碎。
按照位置创建 颗线段树,线段树下标是子弹编号,对于每个位置的子弹,相当于单点修改。
对于木板,就是查询 ,扣除 ,对应区间第 小的位置(子弹编号)。
参考代码:点击
学习完毕
{{ select(1) }}
- YES
- NO
